Bolzano Weierstrass Theorem

Theorem

Any bounded sequence of points in \(\mathbb{R}^{n}\) has a convergence subsequence.

Note that this theorem is for the topology induced by the Euclidean metric. In the context of general topological spaces, this is called the Bolzano-Weierstrass property.

Proof

We first prove the case with \(\mathbb{R}^{1}\) by considering a sequence of real numbers \(\{x_{n}\}_{n \in \mathbb{N}}\).

We define a peak of the sequence to be a point \(x_{k}\) such that:

\[x_{k} > x_{l} \quad \forall l > k,\]

that is, they are greater than the rest of the sequence. Let \(n_{j}\) be the index of the \(j^{\text{th}}\) peak, counting from zero.

Consider the following diagram, where peaks are coloured in green and labelled as described above:

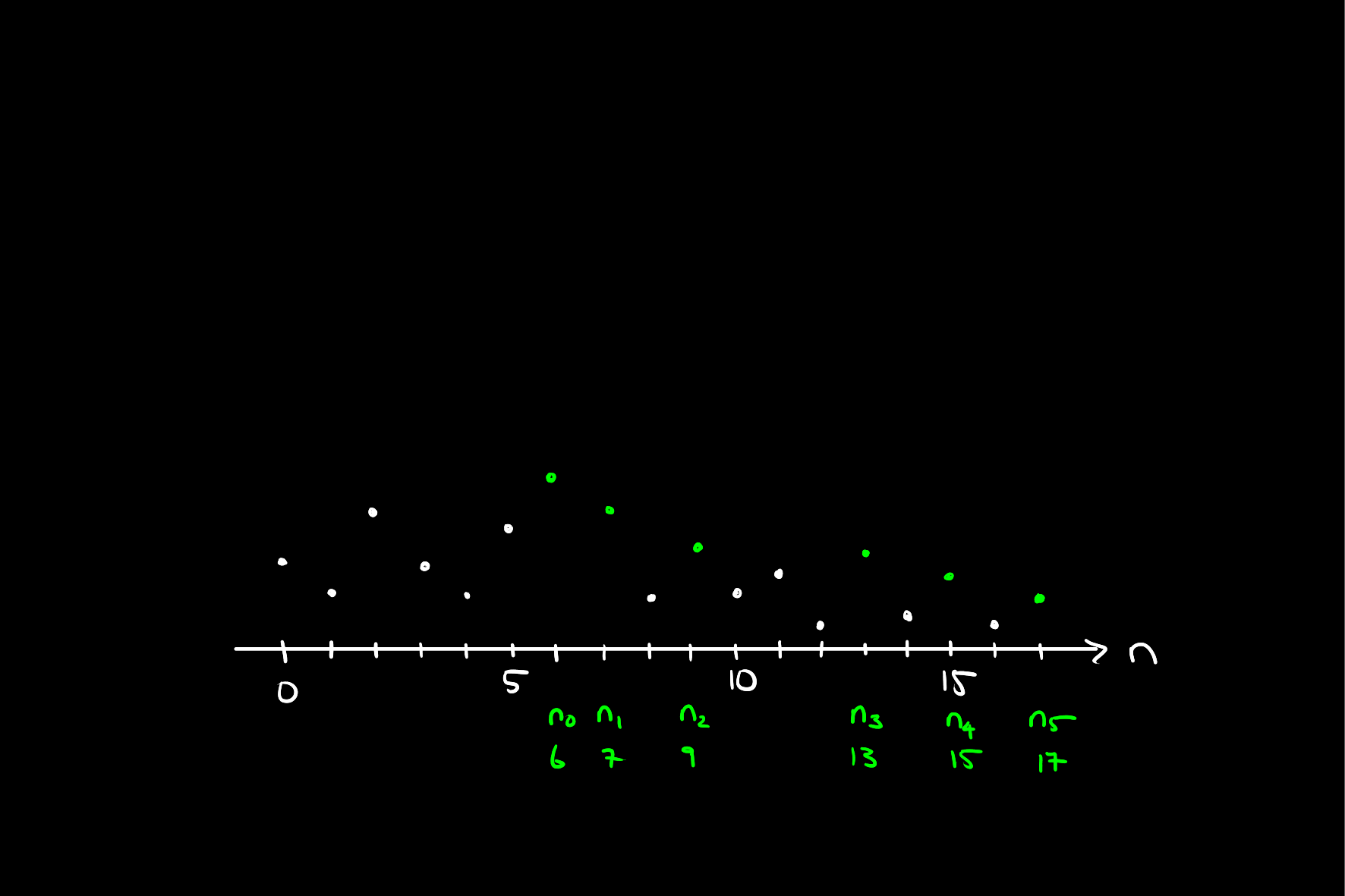
If there are infinitely many peaks, then \(\{x_{n_{j}}\}\) is a monotone subsequence of \(\{x_{n}\}\), in this case strictly decreasing.

If not, then there are finitely many peaks, in which case we let \(N\) be the index of the last peak, or \(N = -1\) if there are no peaks, such as if the entire sequence is non decreasing.

Now, let \(n_{0} = N + 1\). \(x_{n_{0}}\) will be the first point in a new sequence we will construct.

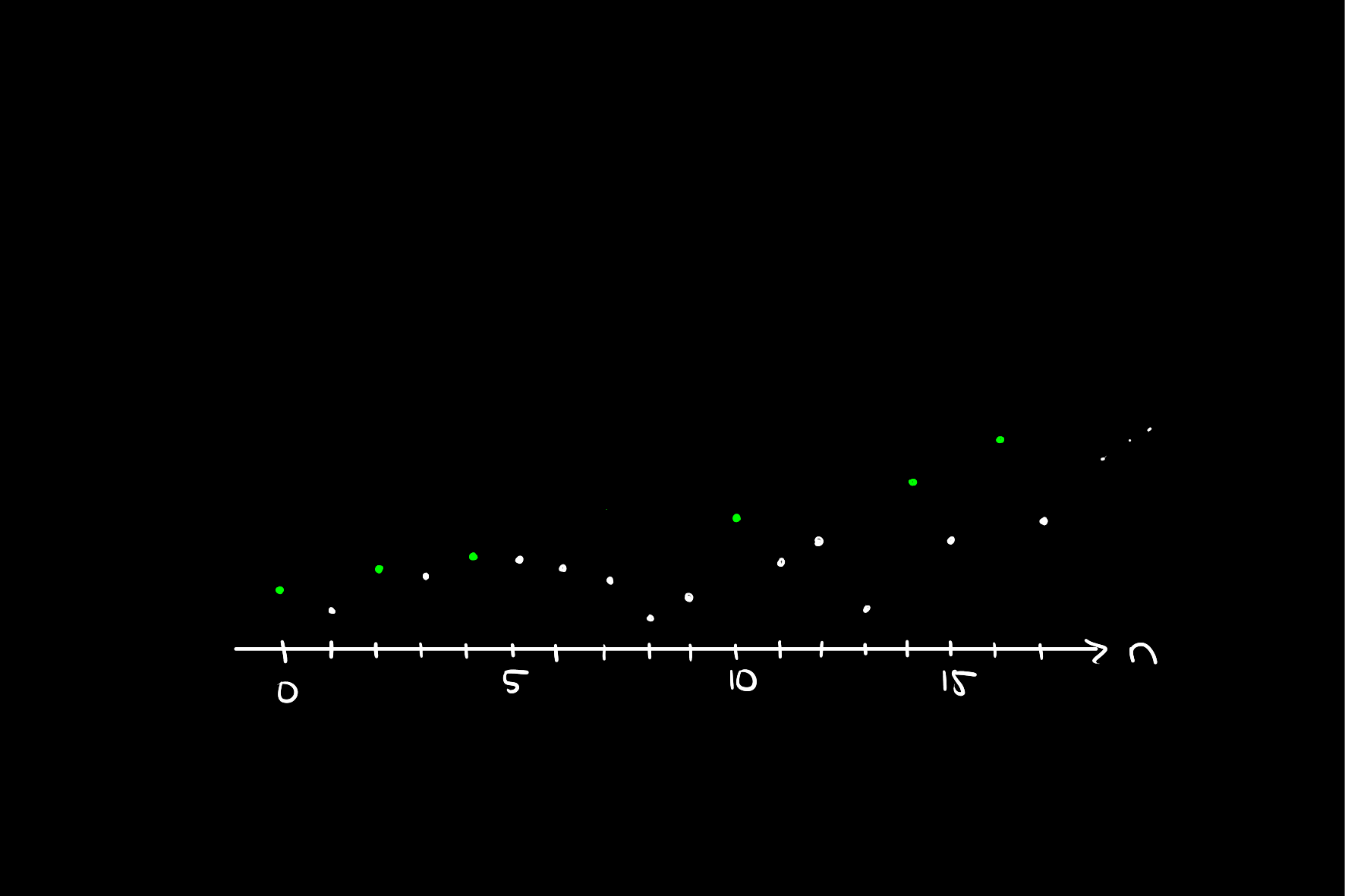
By definition, there are no peaks in the rest of the sequence, and therefore for every point, there must be another greater than or equal to it. That is, there exists an \(l\) such that \(x_{k} \leq x_{l}\) for \(l > k\). We can therefore continually choose such points to get a non decreasing subsequence.

Then, if \(\{x_{n}\}\) is bounded, so are all of its subsequences, and the existence of a monotone subsequence proves convergence from the monotone convergence theorem.

To generalise to \(\mathbb{R}^{d}\), \(\{\boldsymbol{x}_{n}\}\) be a sequence in \(\mathbb{R}^{n}\). We will index each component as \(\boldsymbol{x}^{i}\) to avoid confusion between the sequence index, that is:

\[\boldsymbol{x}_{n} = \begin{bmatrix} x^{1}_{n} \\ x^{2}_{n} \\ \vdots \\ x^{d}_{n} \\ \end{bmatrix}.\]

If we consider the sequence of terms in the first dimension, we can find a convergent subsequence of these terms \(\{x^{1}_{n_{k}}\}\) which directly corresponds with a subsequence of the original sequence \(\{\boldsymbol{x}_{n_{k}}\}\) in which the first dimension's terms converge.

This process can then be repeated, finding a subsequence of \(\{\boldsymbol{x}_{n_{k}}\}\) in which the second component converges, and so on.